One of the major parts of a database management system is query evaluation. A database query q can be evaluated into multiple equivalent queries q'₁, q'₂, ..., q'_n The real challenge is to find the least costly or most efficient query among the pool of equivalent queries.

Conjunctive queries

In relational algebra, a conjunctive queries or CQs can be defined as the following.

In SQL, conjunctive queries correspond to SELECT FROM WHERE queries, where the WHERE conditions contain only equalities. The combined complexity of solving a conjunctive query is NP complete. Some classes of CQs, however, can be computed in polynomial time.

Acyclic CQs

The primary objective of query optimization is to find tractable case CQs. Acyclic queries are the classes of CQs that can be computed in polynomial time. Before diving into the why, let us look at a couple of definitions of acylic CQs.

A more formal definition of acyclic query can be given with the aid of GYO(Graham-Yu-Ozsoyoglu) algorithm. Before that, what is an ear in a hypergraph? An ear in a hypergraph H is a hyperedge e for which we can divide its nodes into two groups:

1. those that appear exclusively in e, and
2. those that are contained in another hyperedge f of H.

Simply, if a hyperedge is isolated, or if it is contained within another hyperedge, it is by definition an ear. Now we are ready to provide the second definition of acyclic CQs.

It's very easy to get lost in words/definitions. GYO reduction is more illustratively defined in the following sections.

The GYO reduction algorithm

The GYO algorithm works as follows:

Illustration of GYO reduction algorithm

Let us consider the following conjunctive query.

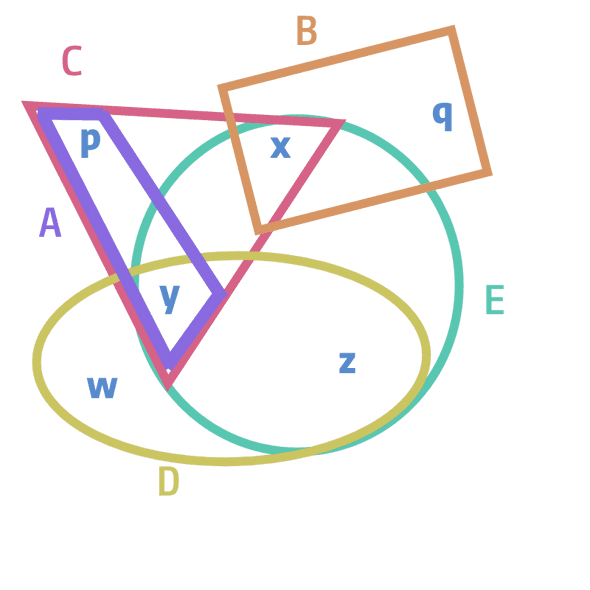
Q:- A(p,y), B(q,x), C(p,x,y), D(w,y,z), E(x,y,z), where for A(p,y), A is a relation whereas p and y are projected variables.

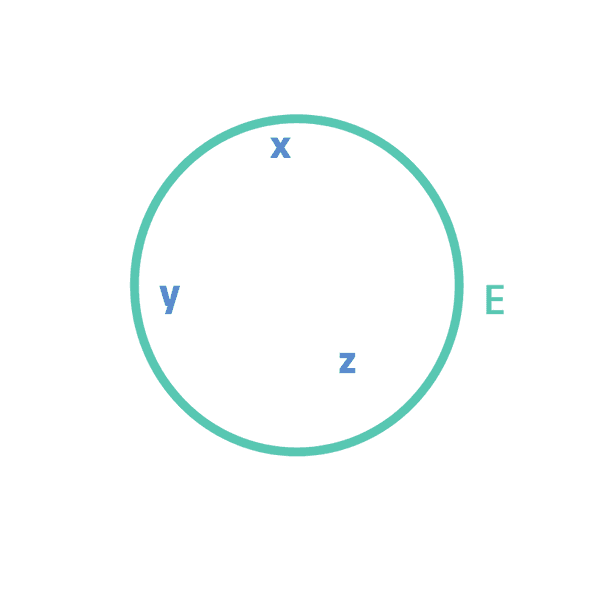
The following is the generated hypergraph for the above CQ. Here the variables are the nodes whereas the relations are the edges.

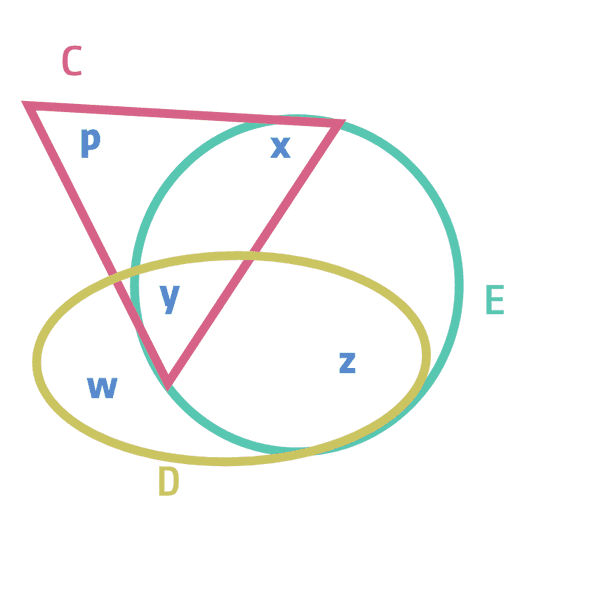
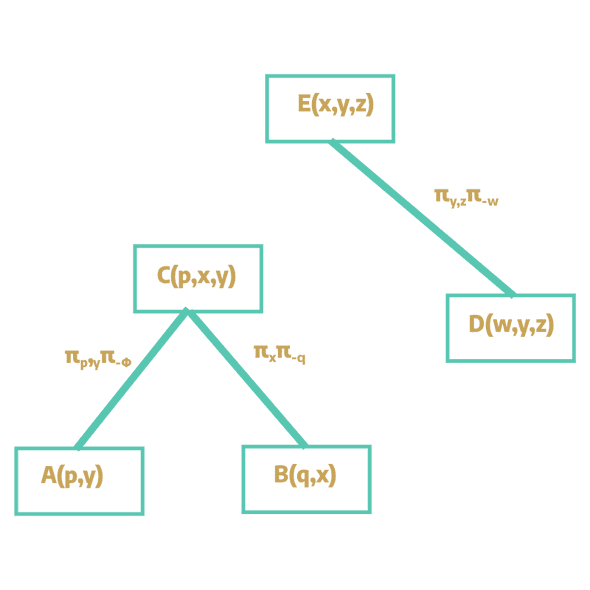
Now let's see the GYO reduction algorithm in place. First let's find the ears in a hypergraph iteratively. Let's see if a hyperedge is isolated or completely contained in another hyperedge. Immediately we can see that for the hyperedge A, both variables p and y are contained within C. Similarly since node q is isolated and when removed the remaining nodes lie within hyperedge C, we are left with the following hypergraph and join tree.

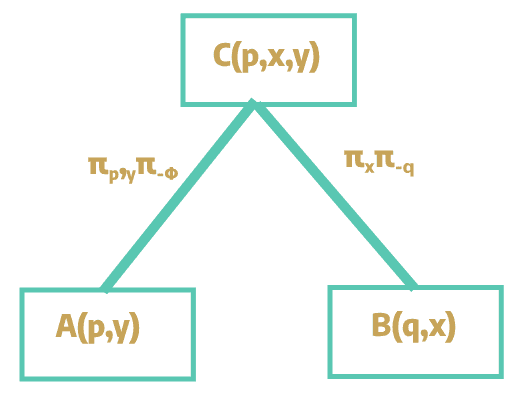
In the join tree, we keep track of the variables that are shared between the atoms. For A(p,y), we can see that it shares both p and y with C(p,x,y). So the join tree tracks π_p,y(π_-Φ). Similar is the case with C(p,x,y) and B(q,x).

In the next pass, we can see node w is isolated, and the remaining node y and z are contained within E, so edge D is consumed. So, by GYO reduction we obtain the following hypergraph and join tree.

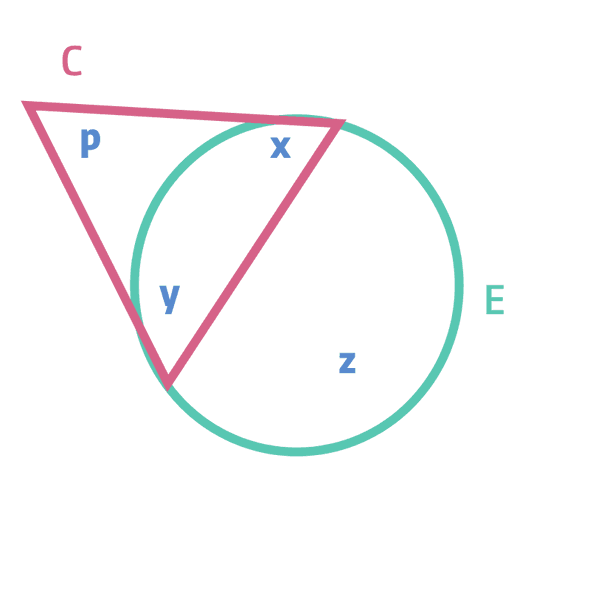
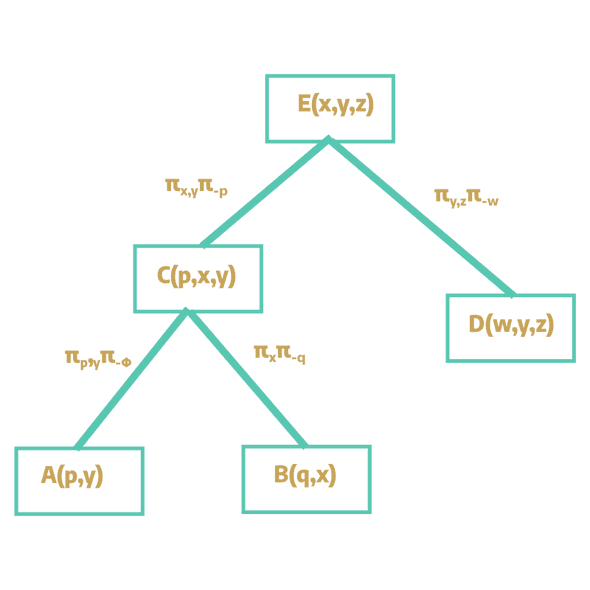
Finally, we repeat this process until we are left with the following hyper graph.

The complete join tree is as follows.

In the next blog, we will discuss the query evaluation part of acyclic queries through Yannakakis algorithm. Until then cheers !!

References

1. Lecture 4: Acyclic conjunctive queries - University of Wisconsin–Madison. (n.d.). https://pages.cs.wisc.edu/~paris/cs784-f19/lectures/lecture4.pdf
2. YouTube. (2022). Toward Responsive DBMS (ICDE 2022 tutorial): Part 3 Acyclic Queries & Enumeration. YouTube. Retrieved May 14, 2023, from https://www.youtube.com/watch?v=toi7ysuyRkw.